Funções

Capítulo 2

Seção 2.7

Funções Pares e Ímpares

Vamos começar a nossa aula, estudando a função par.

Definição:

Uma função é dita par quando f(x) = f(-x) para todo x pertencente ao domínio.

Exemplo:

Vamos trabalhar com a função f(x) = x² - 2.

Agora, usaremos valores de x para calcular a imagem desta função.

Para x = 2, temos f(2) = 2² - 2 = 2 ==> f(2) = 2
Para x = -2, temos f(-2) = (-2)² - 2 = 2 ==> f(-2) = 2
Para x = 1, temos f(1) = 1² - 2 = -1 ==> f(1) = -1
Para x = -1, temos f(-1) = (-1)² - 2 = -1 ==> f(-1) = 1

Observando os cálculos acima, percebemos que f(2) = f(-2) e f(1) = f(-1).
Portanto, para valores opostos de x, temos a mesma imagem. Logo, a função f(x) = x² - 2 é par.

Observe o gráfico desta função abaixo:

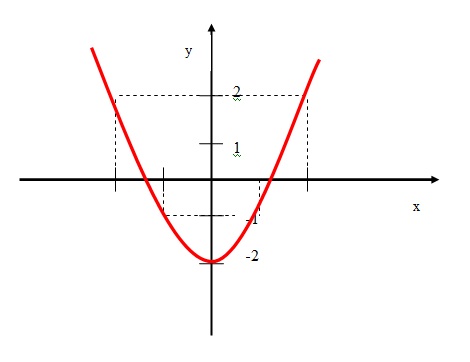
A partir do gr[afico, concluimos que a função f(x) = x² - 2 é simétrica em relação ao eixo y (ordenadas).
Quando isso acontece, podemos dizer também que a função é par.

Função Ímpar

Definição:

Uma função é dita ímpar quando f(x) = -f(-x) para todo x pertencente ao domínio.

Exemplo:

Dada a função f(x) = x

Agora, usaremos valores de x para calcular a imagem desta função.

Para x = 2, temos f(2) = 2 ==> f(2) = 2
Para x = -2, temos f(-2) = - 2 ==> f(-2) = - 2
Para x = 1, temos f(1) = 1 ==> f(1) = 1
Para x = -1, temos f(-1) = -1 ==> f(-1) = -1

Observando os cálculos acima, percebemos que f(2) = -f(-2) e f(1) = -f(-1).
Portanto, para valores opostos de x, temos a mesma imagem para -f(-x). Logo, a função f(x) = x é ímpar.

Observe o gráfico desta função abaixo:

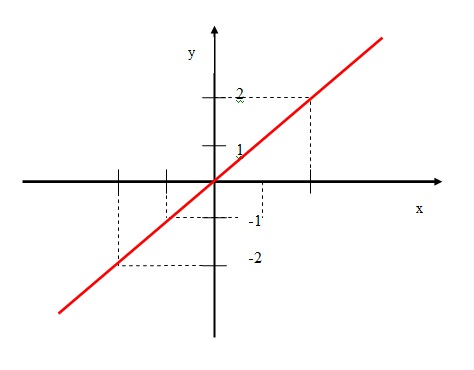
A partir do gráfico, concluimos que a função f(x) = x é simétrica em relação a origem do eixo cartesiano (0,0).
Quando isso acontece, podemos dizer também que a função f(x) é ímpar.