Inequações Modulares

Capítulo 5

Seção 5.3

1) Resolva a inequação |x² - 4x + 2| < 1

Na aula da seção 5.1, nós vimos que quando o |x| < a (para a > 0), temos que - a < x < a.

Logo, temos que -1 < | x² - 4x + 2 | < 1. Portanto, temos duas inequação que são:

a) x² - 4x + 2 > -1
b) x² - 4x + 2 < 1

Vamos resolver a primeira inequação x² - 4x + 2 > -1

Vai ficar:

x² - 4x + 3 > 0.

Resolvendo por Báskara, acharemos as seguintes raízes:

x' = 3
x'' = 1

Agora, resolveremos a segunda inequação x² - 4x + 2 < 1

Vai ficar:

x² - 4x + 1 < 0.

Resolvendo por Báskara, acharemos as seguintes raízes:

x' = 2 + √ 12
x'' = 2 - √ 12

Quando |x| < a, nós fazemos a intersecção dos nossos conjuntos-solução. Logo,


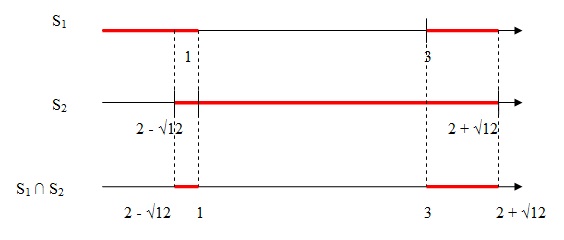
Portanto, o conjunto-solução que procuramos é:

S = { x ∈ IR | 2 - √ 12 < x < 1 ou 3 < x < 2 + √ 12

2) Resolva a inequação |2x - 1| > 3.

Nesse caso, nós temos |x| > a (para a > 0). Logo, temos que x > a ou x < -a.

No exercício 2, temos duas inequações que são:

a) 2x - 1 > 3
b) 2x - 1 < -3

Resolvendo a primeira temos:
2x - 1 > 3 => 2x > 3 + 1 => 2x > 4 => x > 4/2 => x > 2

Resolvendo a segunda temos:
2x - 1 < -3 => 2x < -3 + 1 => 2x < -2 => x < -2/2 => x < -1

Quando |x| > a, nós fazemos a união dos nossos conjuntos-solução. Logo,


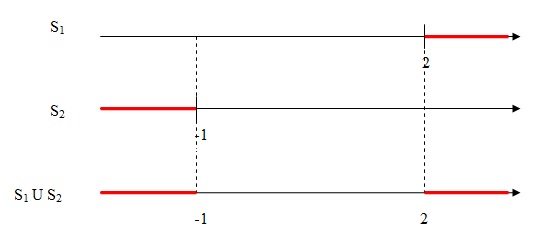
Portanto, o conjunto-solução que procuramos é:

S = { x ∈ IR | x > 2 ou x < -1 }