Inequações-Quociente de Segundo Grau

Capítulo 4

Seção 4.11

Vamos aplicar nas inequações quociente de 2o. grau, o mesmo que aprendemos com as de 1o. grau.

Exemplo:

1) Resolva a inequação-quociente abaixo:

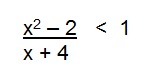
Antes faremos uma pequena transformação:

Agora temos uma inequação com o seguinte formato:

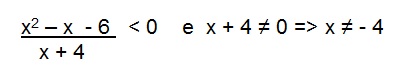
Resolvendo a primeira inequação temos:
1) f(x) = x² - x - 6 > 0

Dados da inequação:

a = 1
b = -1
c = -6

Usando a fórmula de Bhaskara.
Resolvendo Δ, temos:

Δ = b² - 4.a.c
Δ = (-1)² - 4.1.(-6)
Δ = 1 + 24
Δ = 25

Vamos agora achar as raízes:

x = (-b ± √ Δ)/2a
x = (-(-1) ± √ 25)/2.1
x = (1 ± 5)/2

x' = (1 + 5) / 2
x' = 6/2
x' = 3

x'' = (1 - 5) / 2
x'' = -4 / 2
x'' = -2

Esboçando as raízes na reta dos reais com o respectivo sinal da função:



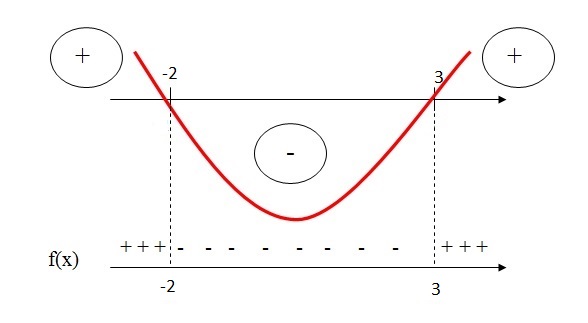
Então, o conjunto-solução desta inequação é:

S = { x ∈ IR | -2 < x < 3 }


2) Resolvendo o outro zero da função, temos:

g(x) = x + 4
0 = x + 4
x = -4

Atenção !!

Aqui nós encontramos o zero da função, mas não podemos esquecer que o x tem que ser diferente de 4 para não zerar o denominador da nossa inequação.

Esboçando o zero da função na reta dos reais com o respectivo sinal da função:



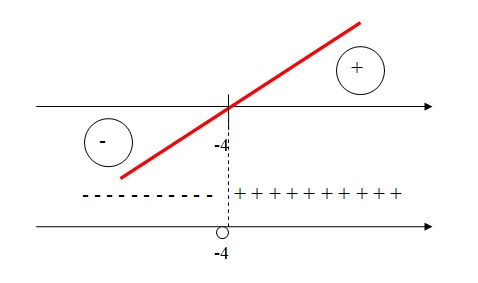
Agora vamos fazer a divisão dos intervalos das inequações para depois achar o conjunto-solução resultante que vai nos dar o resultado dessa inequação-quociente:


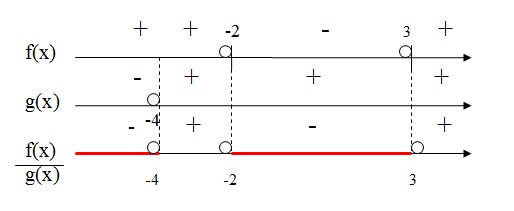
Como a inequação está pedindo valores negativos, ou seja, menores que zero,(f(x)/g(x)) < 0, então nossos valores de x tem que ser menores que zero em intervalos abertos, já que temos um sinal de menor (<).

Olhando para a figura acima, concluimos que o conjunto-solução dessa inequação-quociente é:

S = { x ∈ IR | x < -4 ou -2 < x < -3 }