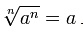Radiciação
A radiciação é uma operação matemática, sendo a raiz apenas uma forma de se representar a potenciação com expoente fracionário.
Exemplo: 52/3 = 3 √ 5 2
Nomenclatura:
√ => radical
5 => radicando
3 => índice da raiz
2 => potência
Observações:
- Quando não aparece o índice no radical, é porque essa raiz é 2. Portanto, é uma raiz quadrada.
- Não existe raíz de número real negativo para índice par.
Exemplo:
√ -16 não existe no conjuntos dos números reais.
- Existe raíz para número real negativo quando o índice for ímpar.
Exemplo:
3 √ - 1 = - 1
Propriedades:

1) Distribui-se o índice para os dois radicandos.
Exemplo:
√ 16.9 = √ 16 √ 9 = 4 x 3 = 12

2)Distribui-se o índice e o radical para o numerador e denominador da fração.
Exemplo:


3) Quando está se extraindo a raiz de outro radical, multiplica-se os índices.
Exemplo:


4) Quando uma raíz está elevada a uma potência “m”, nós elevamos o radicando a essa potência “m”.
Exemplo:
(3 √ 9)2 = 3 √ 9 2 = 3 √ 81 = 3 √ 33 = 3
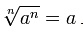
5) Como visto no exemplo anterior, quando temos índice e potência iguais, nós podemos cortá-los e nos restará apenas o radicando.
Exemplo:
6 √ 76 = 7

6) Quandro a potência for uma fração e negativa, isso equivale a escrever a raíz na forma invertida e o radical fica no denominador.
Exemplo:
4-1/2 = 1 / ( √ 4) = 1 / 2
Página Principal