
Teorema de Tales
Tales de Mileto foi um filósofo, astrônomo e matemático grego que viveu na era antes de Cristo.
Ele formulou o seguinte teorema:
“Feixe de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes.”
Essa teoria é mostrada na figura abaixo:
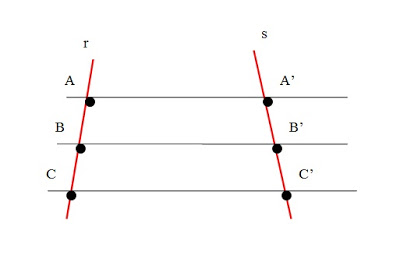
- O segmento de reta AB da reta r é igual ao segmento de reta A’B’ da reta s.
- O segmento de reta BC da reta r é igual ao segmento de reta B’C’ da reta s.
Usando a proporcionalidade, nós temos então:
AB = A’B’
BC B’C’
Exercício:
1) Observando a figura abaixo, utilize o Teorema de Tales para calcular x:

Observando a figura, nós temos que:
- O valor da reta AB é 2x - 8
- O valor da reta BC é x – 2
- O valor da reta A’B’ é 9
- O valor da reta B’C’ é 10
Substituindo na expressão:
AB = A’B’ , temos:
BC B’C’
2x – 8 = 9 =>
x – 2 10
10(2x – 8) = 9(x – 2) => 20x – 80 = 9x – 18 =>
20x – 9x = 80 – 18 =>
11x = 62 =>
x = 62/11
Página Principal



